交际与控制图（CCG，Communicative and Controlled Graph）

　　语言系统，是“单位的（组合/聚合）关系”的系统（索绪尔）。
　　“单位”：可离散化的个体，可类比于社会关系中的个人或团体。
　　“关系”：个体与个体之间存在的联系，可类比于社会关系中人与人之间的各种交际。
　　因此，语言系统可以视作各种语言单位由其交际联系在一起的“语言网络”，从数学角度来看就是一个“点（node）”和“边（edge）”构成的“图（Graph）”，于是：
　　点：语言的句法语义或形式单位，个人，团体；
　　边：语言单位之间某种可观察到的联系，个人之间的交流，团体之间的交流等。
　　例子：Cysouw（2003）将世界语言中的“人称”语义分离出8种语义单位，即8个点：

　　边则表示：某一人称词所“包含“的人称语义单位情况，或者说，人称语义单位在不同语言形式中的“共现”情况。如：
　　汉语的“人家”，可以指第三方，也可以指说话人。那么“人家”这一形式就包含了两个人称语义单位“1、”，即“1、3”共现，可画“边”相连为“1-3”。
　　将考察范围内的“点”按调查情况连“边”为“图”的一个重要目的，就是研究“图”所示的“规则”。
　　即研究“图”所示的“控制”情况。

显性控制与隐性控制

　　显性控制：一旦系统成员产生明确的关于某种运行规则的认识时，这一规则便“外化”于该社会，成为一条显性的机制，从而得以在纷繁复杂的社会事件中保持相对独立、静止的面貌，并反过头来要求社会必须遵从于它。
　　社会关系中来说，就是被加冕为王，有了王冠和“大义名分”，从而用法律和最大的权力来要求所有人遵循其守则。
　　语言系统中，明确的“形式标记”就是显性控制的体现，标记必须出现就是外化的显性规律。
　　隐性控制：在显性化之前，一个未曾事先规定任何规则的社会，在其自身的运行中仍然会自发地形成一套运行机制，但它仅仅是现在的、当下的、自动地形成着的，每一个人都卷入其中，而未必知道它，“不识庐山真面目，只缘身在此山中”。
　　社会关系中几乎任何一个社团都存在这样的隐性中心，如一个朋友圈里的核心成员和他的亲密圈子，如国王身边若干个最具有影响能力的大臣集团。甚至这个隐性中心未必是“强势”的，如通常情况下，一个家庭有了小孩以后，恰恰因为小孩极弱极需要依赖旁人照顾，反而使得父母的“二人空间”大大减少而一切家庭活动多是围着小孩在转，从而小孩成为了自然的“家庭中心”。
　　语言系统中，凡是没有被“形式标记”明确化的一切控制都是隐性控制。同样的，隐性中心不一定“强势”，实际上语言系统中居于句法上位的功能性成分往往显得“弱势”，但正是因其“依赖性强独立性弱甚至极弱”，功能性成分得以联系独立性相对强的实词成为句法中心。
　　研究“图”总是为了研究“隐性控制”。

隐性控制的来源：图的“不均匀”和“回路”

最典型的“无控制”是团（clique）。团是指三元或三元以上的完全图（complete graph），其中任意两点之间都可以“直接、均匀”相连的“完全回路”，因此最终来说任意两点间都是绝对“平等”的，自然没有任何“控制”关系。

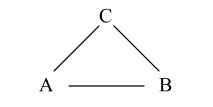
　　在社会关系中，则是某种“理想的乌托邦”，某种个体间绝对“平等、公平、平均、均匀”的社会。但通常是不现实的。
　　现实中的实际情况往往是：社会中各种关系是“不均匀”的，因此形成的“图”也是不均匀的。考察图的“关系疏密”，就可以得到社会中各种隐性控制情况。
　　同样，在理想情况下：
　　最典型的“控制中心”是辐射状星型图的中心，其中A点作为辐射中心，其他所有点都只和A点直接交际，因此A拥有绝对的控制地位。
　　最典型的“控制路径”则是树（tree）图，其中各点的控制层级分明，上级控制了他的直属下级，没有控制“回路”。树的特例是“链”，即所有节点相继首尾相连且没有回路。

　　　　　　

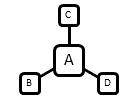
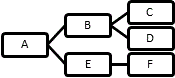
　　当然这种“理想的最典型的”控制也往往是不现实的，如果可以因为社会关系的复杂性，隐性控制往往表现出“有回路”的形式。
　　这是隐性控制的“隐蔽”性，无法直接定性描写，只有用定量来做研究。但是隐性的内部控制很难把握，它具有模糊性、即时性、变化性等特征，而且亲身经历它的人也往往缺乏共识。所以对隐性控制的探索至少要衡量两点之间的平衡：
　　1、概括充分：隐性控制难以识别，调查数据一旦纷繁复杂而算法过于简单，可能根本概括不出什么规律来，因此需要有能够进行概括的算法。
　　2、概括适度：同时，隐性控制又总是处在形成的过程中，如果控制机制本身不强，过强的识别算法反而会坏事。“过犹不及”，又称为“过度理解”（over-understanding），它与“错误理解”（mis-understanding）一样，都是对事实的非真实的反映。

CCG的前身：语义地图（Semantic map）

　　该理论最初的目的是为了研究跨语言的互相有“功能”联系的多个形式间的蕴含共性。其中：
　　点：语言学家针对某一语言范畴所分解的语义语用单位。
　　边：语义语用单位在不同语言形式中共现的的情况。
　　蕴含共性：通过各语义语用单位的复杂共现，绘制成“图”，通过图的不均匀，提取图中各语义语用单位的控制关系。
　　例如：某语言范畴可分解出3个语义单位：A、B、C。在4种语言中L1-L4，每种语言各有形式能够表达不同的语义单位，形成不同的共现关系。

	A	B	C
L1	X1	X2	X3
L2	X4	X4	X5
L3	X6	X7	X7
L4	X8	X8	X8

L=语言；X=形式；A、B、C=功能

　　L1：A、B、C各自由不同的形式表达，无共现，是独立的，因此没有边连接。
　　L2：A、B合用一个形式，共现可连边，C独立。
　　L3：A独立，B、C合用一个形式可连边。
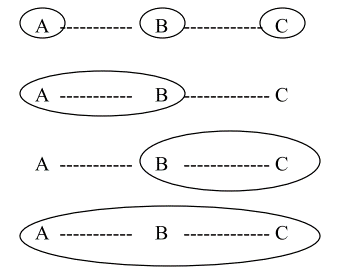
　　L4：A、B、C一起合用一个形式，共现可连边。这时，因为是3个点共现，连边的情况就变得复杂起来，因为3个点连在一起，其实有多种连接子图：

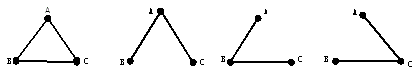
　　语义地图研究中，采用的连边策略如下：
　　因为前述L2和L3的两两共现中，有A-B和B-C共现，无A-C共现，因此如果假定这个考察已经足够充分，那么A、B、C三者的共现是通过“A-B-C”连边实现的（上述第3个子图），即A通过B联系到C而A、C之间没有直接联系。
　　这就意味着：
　　控制路径为：A-B-C的链式控制，B是控制中心。
　　蕴含关系为：如果一个语言形式能表达语义A、C，那么就一定能表达语义B，不存在只表达语义A、C而不表达B的语言。
　　从社会学来看，假设A\B\C为三个人，经常去同一个俱乐部，有时候是A和B的“二人世界”，有时候是B和C的“二人世界”，有时候三个人都会同时出现，但A和C从来没有“二人世界”过。了解了这种情况，我们一般会判断：B分别和A、C是朋友，A和C则关系疏远，三人同时出现时应该是B分别联系了A和C邀其同往的。
　　这一语义地图绘制方式，为简单情况下的“理想绘制方式”。

带权重的复杂CCG

　　上述语义地图是简化的，各点之间连边只有“有无”之别。
　　现实中，各点之间的联系不是简单的“有无”，而是更复杂的“轻重”不同。
　　例如：张三、李四、王五三个人同时出席俱乐部的情况如下：
　　张、李“二人世界”25次；李、王“二人世界”37次，都较多；
　　张、王“二人世界”3次，虽然不是没有但是相对少得多。
　　一般我们会判断：李和张、王分别是朋友，关系较密切；张和王之间大约认识但是基本保持“点头之交”的程度，关系较疏远。
　　因此三人同时出席时，多半还是李分头联系了张和王，李是三人的中心。
　　做一个预测的话，未来一年中，其他条件不变的情况下，某次活动“有张、有王、无李”的概率肯定较低。
　　从蕴涵共性上看，依旧倾向于“张、王的存在”就大概率蕴涵了“李的存在”。

　　更复杂的情况：复杂共线：多点，多种共现情况，每种共现的区别不是“有无”而是“频次”轻重不同。
　　例如：Cysouw（2007：19）人称8个基元共现的频次表

现有5种加权生成CCG的算法思路

完全加权：Cysouw（2007：19）

　　1、如果基元a、b两两共现，就将两个基元之间连上一条边a-b，且为这条边加上共现频次fab为权重为；
　　2、如果基元a、b、c三者共现，就认为它们两两之间全部存在同一关系，于是两两之间全部连上边，一共是3条边a-b、b-c、a-c，同时为3条边都加上fabc为权重；
　　3、以此类推，如果n个基元共现，就认为它们两两之间全部存在同一关系，于是连接上所有n*(n-1)条边，同时为所有n*(n-1)条边都加上fn为权重。
　　特点：
　　1、 对每行数据的局部而言，任意两点之间都有直接联系的完全图；
　　2、 不兼容语义地图理想绘制方式；
　　3、 概括性不足，Cysouw（2007：19）的人称语义示例中，所有点之间都有连线。在研究人称语义相关蕴含共性的简图中，大量权重重的边被删除了，权重轻的边得以保留，没有一个可操作的简图（控制关系提取）算法。

完全关联：郭锐（2012：115-116）

　　关联度公式：A ＝ S1•S2／（W1＋W2－S1•S2）×100
　　其中，“S1•S2”指基元1和基元2在数据中“任意”共现的频次，W1指具有义项1的总频次，W2指具有义项2的总频次。简单地说，就是将完全加权按一定比例缩放，也是把每一个记录局部视作完全图，计算的是一种“完全关联度”。
　　特点：
　　1、 对每行数据的局部而言，任意两点之间都有直接联系的完全图；
　　2、 不兼容语义地图理想绘制方式；
　　3、 概括性不足，人称语义示例中，所有点之间都有连线。在研究人称语义相关蕴含共性的简图中，一些权重重的边被删除了，权重轻的边得以保留，没有一个可操作的简图（控制关系提取）算法。

赢家通吃：陈振宁、陈振宇（2014）

　　1、两两结对，形成n*(n-1)个对子；
　　2、查其他所有记录，计算每个对子的独立两两共现频次；
　　3、按独立两两共现频次在对子之间竞争；
　　4、前n-1个频次大的对子成为“赢家”，其余“输家”；
　　5、赢家连接，都获得本记录的100%加权；
　　6、输家什么都没有，不连接，不加权。
　　特点：
　　1、对每行数据局部而言，按全部的“独立两两共现频次”进行筛选，输家没有连线，不是完全图；
　　2、兼容语义地图理想绘制方式；
　　3、概括性强，只要是输家就难以获得权重，最终各步“输家”的权重累加少，可以直接按权重轻重设计算法，删除回路得到简图（控制关系提取）。

赢家多吃：陈振宁、陈振宇（2014）

　　1、计算所有两两对子的独立共现频次之和sum（f_独）；
　　2、赢家对子连接，按比例分配加权，即每个赢家对子得到的加权为：f_独i/sum(f_独)；
　　3、输家对子还是不连接，加权为0。
　　特点：
　　1、对每行数据局部而言，按全部的“独立两两共现频次”进行筛选，输家没有连线，不是完全图；
　　2、兼容语义地图理想绘制方式；
　　3、概括性强，只要是输家就难以获得权重，最终各步“输家”的权重累加少，可以直接按权重轻重设计算法，删除回路得到简图（控制关系提取）。
　　4、赢家内部分化更明显。

赢多输少：陈振宁、陈振宇（2014）

　　1、计算所有两两对子的独立共现频次之和sum（f_独）；
　　2、赢家对子和输家对子都可以连接，按比例分配加权，即每个赢家对子得到的加权为：f_独i/sum（f_独）；
　　特点：
　　1、对每行数据局部而言，按全部的“独立两两共现频次”进行筛选，绝对输家没有连线，不是完全图；
　　2、兼容语义地图理想绘制方式；
　　3、概括性中等，小赢家和输家获得权重小，按权重轻重设计简图算法，删除回路得到的简图（控制关系提取）较完全二算法明晰。
　　4、可能避免“过度概括”，赢家输家之间层次差异更细微，简图算法中的被删除边如果权重较大，可以直接判定为“必须保留的回路”。

CCG的控制关系提取算法：陈振宁、陈振宇（2014、2015）

最大简图

　　基本思路：按权重轻重，将所有回路尽可能删除（只有在权重相等的“歧义”情况下无法删除回路），即得到无回路的最大“树”。从而得到各点之间概率最大的控制关系。
　　1、 将CCG各边权重按从小到大顺序排列：
　　2、 从最小权重边开始检查，如果该边形成回路且没有歧义，则删除；如果该边不形成回路或者该边对其他边来说存在歧义（权重相等），则保留；
　　3、 重复2，直到处理完所有边；
　　4、 3所保留的边构成最大简图。

最小简图：

　　基本思路：各点选择“自己控制最严密”的唯一一条边（只有在权重相等的“歧义”情况下才选择多条边），即得到无回路的最小“树”。从而得到各点之间概率最大同时唯一的控制关系。
　　1、 检查CCG第一点，在该点所连各边中，选取权重最大的边，如权重最大边有多条则选取多条；
　　2、 重复1，直到处理完所有点；
　　3、 2所选取的边构成最小简图。

CCG的控制度

　　简图代表了从CCG全图中提取的控制关系。这些控制关系和全图比较，我们就能得到研究的系统的隐性控制程度弱度量D。
　　D=（SUM（w简）-SUM（w简·歧））÷SUM（w全）
　　其中，w简表示简图的全部权重之和，w简·歧表示简图中歧义边的权重之和，w全表示全图的权重之和。
　　1、在最理想情况下，如果生成的CCG全图本身就是一个能够表达典型控制关系的树，那么简图和全图完全重合，且无歧义、无回路，分子分母相等，控制度100%；
　　2、相反的最理想情况下，CCG是完全图且各边都有相同权重，从而形成了回路，且因为回路上各边是权重相同的“歧义边”，所以无法删除，得到的简图和全图也是完全重合的。但“简图”不“简”，本身依旧是充满回路或“歧义”的图，所以SUM（w简）= SUM（w简·歧），则分子为0，控制度还是为0；
　　3、其他情况下，控制度的分子是简图内的无歧义边的权重比例，这一比例越高，考察范围内的系统隐性控制程度或者说规约程度就越高。